On Randomness
By Fernando Rodriguez Villegas
- Categories: Writing
Iperborea is an italian publishing house founded by Emilia Lodigiani in 1987 which aims to bring to Italian readers the literature of northern Europe. Their books have a distinctive format and texture of their covers making them instantly recognizable while browsing in a bookstore. Not all of their titles are easy to find in English in Italy so they are a good way for me to connect to Scandinavian culture while also practicing my Italian. I read about the incredible Lake Nyos disaster in Cameroon for example, in Il Enigma del Lago Rosso by Frank Westerman (translated from the Dutch); there is also an English translation: Choke Valley.
I picked up Orden som formade Sverige by Elisabeth Åsbrink in Italian at the Minerva bookstore in Trieste. The literal translation of the title is The words that shaped Sweden and has actually been translated to English as Made in Sweden: 25 ideas that created a country but I am reading it in Italian (Made in Sweden: le parole che hanno fatto la Svezia).
The book consists of short chapters discussing some event of the history of Sweden, centered around language or culture in some way, ordered chronologically. I found the style, pace and perspective in each topic captivating.
There is the amazing story mentioned in passing (in Chapter 1) of runes inscribed in a marble sculpture of a lion once in the port of Piraeus in Greece and now in the Arsenal in Venice. The text was carved in the 11th century and is now so weathered down that reading it is a huge challenge. Various reconstructions exist but whatever the precise meaning it is clear that it is basically just like a modern grafitti of the sort X and his pals were here, written by a bunch of early Swedes far from home and with time to kill. I will come back to runes in another post as they were important to me as a kid via Voyage to the Centre of the Earth of J. Verne .
But the main story for this post is in Chapter 6 about the Kalmar Union. This is a major event in the history of Scandinavia of the late 1300’s where the kingdoms of Denmark, Norway and Sweden were joined under a single monarch. Erik Gustaf Geijer an early 1800’s Swedish writer, historian, composer famously said that the Kalmar Union was
…an event that looks like an idea.
I was struck by this because it sounds exactly what Darwin would say about life. Life is a random event that looks intentional, like someone, a conscious being, intended it, wanted it. Randomness that looks like volition.
But then again this is hard for us humans. Our brain evolved to look for patterns and extract meaning. A piece of marble in form of a lion with carved symbols that look like a message in an unknown language cannot just be random (monkeys with a typewriter notwithstanding).
It is hard for us to understand what random means. A common exercise in a lecture on probability is to divide the class in two and ask one group to toss a coin 100 times recording the outcome and the other to write down a made-up sequence of such tosses. Typically, it is later easy to figure out which sequence came from the actual coin flips: the one that includes strings of six heads in a row.
Benford’s Law is the observation that in large data sets of unstructured numbers the distribution of their first digits among $1,2,…,9$ is not actually uniform but logarithmic. Concretely, the proportion of numbers in the data set with a given first digit $d$ is roughly the length of the interval $[\log(d),\log(d+1)]$.
The story of Benford’s Law is interesting and starts with a paper by Simon Newcomb in 1881:

It was however F. Benford with his 1938 paper published in the Proceedings of the American Philosophical Society (!)

that really got people’s attention and ended up with his name associated with the phenomenon. Benford seems to have been unaware of Newcomb’s paper.
Newcomb writes:
That the ten digits do not occur with equal frequency must be evident to any one making much use of logarithmic tables, and noticing how much faster the first pages wear out than the last ones. The first significant figure is oftener 1 than any other digit, and the frequency diminishes up to 9. The question naturally arises whether the reverse would be true of logarithms.
and gives the following table

(To me, Newcomb’s is a beautiful example of being alert to and curious of the unexpected while doing something totally unrelated.)
Benford’s Law is important if you are trying to make a whole bunch of numbers up. For example, if you are making up the cost of non-existent expenses that you would like to claim your employer. Apparently, most people make numbers up in ways they believe are random but that fail miserably to follow Benford’s Law (and this remains true even if you convert the fake expenses to a different currency or change from base ten to any other for that matter). Like thinking that 6 heads in a row in 100 coin tosses cannot be random.
Conversely, the law is also useful if you suspect that a list of numbers, again, say expenses from a long business trip, were fabricated. Applying these distribution ideas is one of the tools of what is known as forensic accounting, a mathematical component of financial fraud detection.
In a different, more topical use, it was discovered in a 2015 experiment that a small percentage of Twitter accounts in a large sample (those with at least 100 friends) were actually bots. The paper’s author, the computer scientist Jennifer Golbeck, checked whether the number of friends of the friends of the sampled account followed Benford’s Law. Most did, the bots did not.
For fun while writing this I did the following test. I took the size of the around 250 files and sub-folders in my laptop’s Documents folder and computed the frequency of their first digits. Plotted against Benford’s prediction gives this
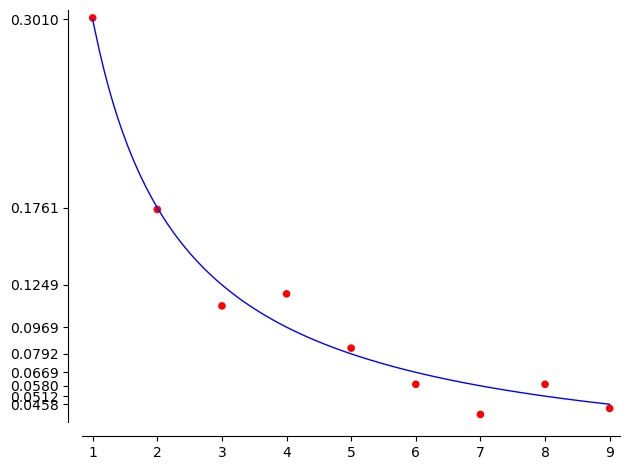
That’s a pretty decent agreement.
At the time I learned about Benford’s Law my youngest daughter Lula had to present a project for the Science Fair at her school in Austin. It was in fact the last such project for either of my kids. Malena was already in middle-school and Lula was in the last year of elementary school.
My kids had never done well at Science Fair projects. I always felt that it was one important american cultural marker that I failed to engage with. Typically, parents, mostly fathers it would seem, work intensely with their kids on their projects and these become pretty competitive affairs.
I suggested Lula that she collected data from family friends, teachers and neighbors asking them to produce digits in three different ways. First, by asking them the town or country where one of their grandparents was born, from which we then recorded the first digit of its current population. Second, by choosing a digit at random. And third, by spinning a wheel divided into 9 sectors and labeled 1 to 9. The contrast in the results were quite striking even in the small sample she collected and the population first digits followed Benford’s Law quite well.
We saved the family honor. Lula’s project got a 1st place purple ribbon and was selected to participate at the city level competition (but that was as far as things went).